
Metoda wieloparametryczna RS
Metoda wieloparametryczna oparta o algorytm Range Searching (zwana dalej metodą RS) selekcji CC i NC polega na klasyfikacji przypadków w wielu wymiarach jednocześnie [17] [18] [19]. Poniżej przedstawiony został przykład dwuwymiarowy.
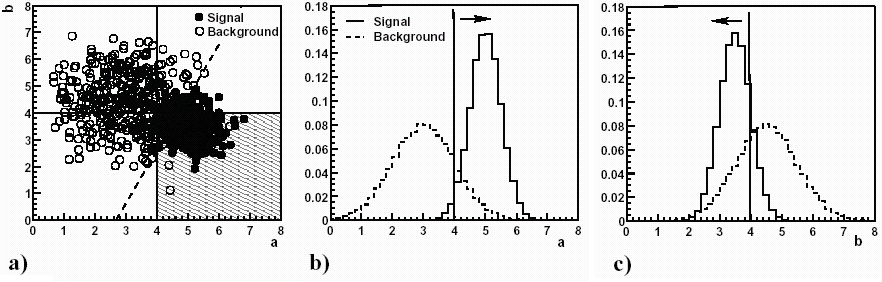
Rozważmy pewien rozkład przypadków na płaszczyźnie we współrzędnych a-b (rys. 5.20a). Na rysunkach 5.20b oraz 5.20c widać rzuty przypadku na daną oś w formie histogramu. Jest to klasyczny przykład metody cięć, kiedy to klasyfikujemy przypadki sygnału (ang. signal, ciągła linia) od tła (ang. background, linia przerywana) w oparciu o pojedynczą zmienną. Cięcia zaznaczono pionową kreską i strzałką. Dzięki temu wyselekcjonowany został obszar oznaczony na rys. 5.20a na szaro. Widać zatem, jak duża część przypadków sygnału jest tracona. Gdyby zastosować cięcie z uwzględnieniem dwóch wymiarów (linia przerywana na rys. 5.20a), czystość i efektywność selekcji mogłaby wzrosnąć.
Rysunek 5.20: a) dwuwymiarowy rozkład przypadków tła (ang. background) i sygnału (ang. signal) z zaznaczonym linią przerywaną cięciem; b) rzut rozkładu na oś a; c) rzut rozkładu na oś b [17]
 |
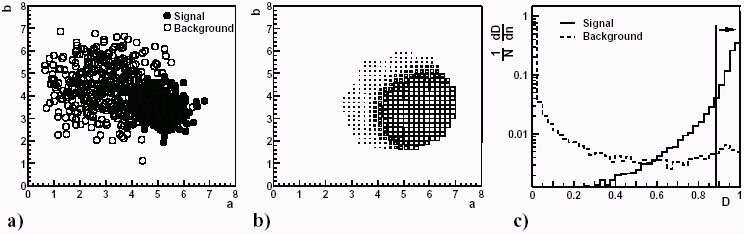
Metoda RS polega na znalezieniu i analizie mapy rozkładu gęstości prawdopodobieństwa występowania przypadków tła i sygnału. Każdemu rozkładowi (rys. 5.21a) przypisać można pewną mapę prawdopodobieństwa znalezienia sygnału (rys. 5.21b). Na tej podstawie sporządzić można rozkład funkcji prawdopodobieństwa D (rys. 5.21c) w oparciu o który, dokonując jednego cięcia, można odseparować przypadki tła od sygnału.
Rysunek 5.21: a) dwuwymiarowy rozkład przypadków tła (ang. background) i sygnału (ang. signal); b) odpowiadający mu rozkład prawdopodobieństw występowania sygnału (rozmiar punktu); c) rozkład zmiennej dyskryminującej D z zaznaczonym cięciem [17]
 |
W niniejszej metodzie zastosowano tzw. algorytm Range Searching4 (z angielskiego przeszukiwanie zakresu), skąd skrót RS. Został on sprawdzony i wykorzystany między innymi do analizy danych w niemieckim ośrodku badań jądrowych DESY w Hamburgu. Charakteryzuje się przede wszystkim bardzo szybkim i sprawnym przeszukiwaniem przypadków oddziaływań, co jest niezwykle istotne, gdy ich liczba przekracza kilkadziesiąt tysięcy.
W celu zastosowania tej metody do separacji przypadków CC i NC w eksperymencie MINOS, w pierwszej kolejności należy stworzyć tzw. wzorzec, którym są dwa pliki binarne (osobno dla CC i NC) zawierające informacje o każdym przypadku po kolei w postaci wartości trzech zmiennych (współrzędnych) - tych samych, które były użyte w metodzie cięć (rozdz. 5.4). Dokładny algorytm programu do tworzenia wzorca znajduje się w dodatku C. Dla potrzeb niniejszej pracy stworzono oba pliki dla 220000 przypadków MonteCarlo. Duża statystyka jest niezbędna dla prawidłowego działania programu, gdzie liczy się duża gęstość przypadków. Każdy wczytany przypadek jest ściśle określony w przestrzeni trzech zmiennych wejściowych poprzez ich wartości. Cała przestrzeń podzielona jest na charakterystyczne komórki o objętości V. Ich rozmiar musi być tak dobrany, aby średnia liczba przypadków przypadających na jedną komórkę nie powodowała zaburzeń. Mniejsza niż 20 wartość spowodowałaby znaczący wzrost znaczenia fluktuacji statystycznych i spadek jakości selekcji. Z kolei efektem za wysokiej liczby przypadków jest zbyt niska rozdzielczość, co również osłabia selekcję [17] [18] [19].
Mając gotowy wzorzec można przejść do właściwego algorytmu. Na początku należy wczytane przypadki z plików wzorcowych o zadanych zmiennych-współrzędnych uszeregować w drzewach.
Rysunek 5.22: Ilustracja obrazująca ideę działania algorytmu do szeregowania przypadków w przestrzeni zmiennych x-y (a) w odpowiednim drzewie binarnym w zależności od wartości współrzędnych x i y (b) [17]
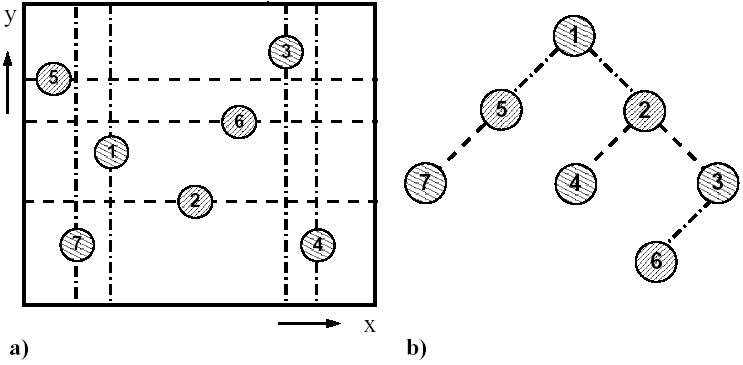 |
Na rysunku 5.22 przedstawiono sposób ustawienia siedmiu przykładowych przypadków w drzewie binarnym (5.22b). Każdy przypadek posiada współrzędne, dzięki którym może zostać przedstawiony w postaci punktu w przestrzeni x i y (rys. 5.22a). Użycie tego przykładu ma na celu objaśnienie idei działania algorytmu, gdyż we właściwej selekcji CC/NC wykorzystane są trzy zmienne. Pierwszy przypadek przykładowy e1(x,y) (kolejność występowania w pliku wzorcowym) staje się automatycznie głównym węzłem drzewa (5.22b). Drugi przypadek e2(x,y) posiada większą współrzędną x niż e1, co powoduje utworzenie nowego węzła e2 poniżej na prawo od e1. Gdyby współrzędna ta była niższa, wówczas nowopowstały węzeł znajdowałby się z lewej strony drzewa. Kolejny węzeł, e3(x,y), również posiada większą współrzędną x niż węzeł e1, więc powinien być także przyłączony na prawo od e1. Jednak pozycja ta jest już zajęta przez e2, więc porównuje się współrzędne y między przypadkami e2 i e3. Węzeł e3 posiada większe y niż e2, więc dołączany jest poniżej na prawo od węzła e2. W przeciwnym wypadku e3 byłby przyłączony na lewo. Rozumując analogicznie, algorytm porządkuje wszystkie przypadki po kolei w drzewa, osobno dla NC i osobno dla CC, poprzez porównywanie współrzędnych x i y (w ogólności może być dowolna liczba współrzędnych). Każde drzewo składa się z pięter, w którym rozpatrywane są najpierw współrzędne x, później y, następnie ponownie x i tak dalej. Całkowity czas potrzebny do wypełnienia drzewa wyraża się wzorem ∼log(i!), gdzie i oznacza ilość węzłów [17]. Po utworzeniu obu drzew na podstawie danych z dwóch plików wzorcowych (w naszym przypadku użyto 3 współrzędnych), program przechodzi do analizy właściwej.
W dalszej kolejności, stosując algorytm podobny do metody cięć, wczytujemy po kolei przypadki, które chcemy zakwalifikować jako CC bądź NC. Dla potrzeb niniejszej pracy użyto ok. 57000 przypadków MonteCarlo. Należy zwrócić uwagę, iż przypadki te muszą być różne od tych użytych do tworzenia wzorca. Po wczytaniu danego przypadku i ustaleniu jego współrzędnych (trzech zmiennych wejściowych), rozpoczyna się przeszukiwanie drzew zawierającego przypadki wzorcowe. Algorytm ten jest analogiczny do algorytmu szeregującego przypadki w drzewach. Następuje przeszukiwanie drzew poprzez porównywanie współrzędnych x, y i z z szybkością ∼log(n), gdzie n oznacza liczbę węzłów (tożsamą z liczbą przypadków MonteCarlo w plikach wzorcowych). Algorytm znajduje przypadki w obszarze V wokół danego punktu i zlicza liczbę przypadków CC oraz NC. Na podstawie stosunku ilości oddziaływań CC do NC określa się zmienną ![]() :
:
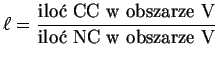
Na podstawie zmiennej ![]() wyznacza się prawdopodobieństwo znalezienia przypadku D w danej komórce V:
wyznacza się prawdopodobieństwo znalezienia przypadku D w danej komórce V:
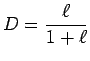
Stosując w algorytmie pętlę po wszystkich wczytywanych przypadkach, otrzymujemy dla każdego indywidualną wartość D w oparciu o drzewo wzorcowe. Selekcję sygnału (CC) od tła (NC) uzyskuje się za pomocą jednego cięcia na rozkładzie D. W sytuacji, gdy liczba przypadków sygnału i/lub tła w komórce V jest za mała, wówczas D przyjmuje domyślną wartość 0, 0.5 lub 1.
komentarze
Copyright © 2008-2010 EPrace oraz autorzy prac.