
Algorytm selekcji
Głównym celem niniejszej pracy jest stworzenie algorytmu selekcjonującego przypadki NC i CC [Dodatek B]. Do tego celu niezbędne jest użycie wspomnianych już symulacji Monte Carlo. Tylko w ten sposób można jednoznacznie stwierdzić, czy dana selekcja jest poprawna czy nie - poprzez sprawdzenie, czy przypadki oznaczone jako kandydaci na dany typ CC/NC są nimi w rzeczywistości. Więcej na temat kryteriów oceny poprawności selekcji znajduje się w rozdziale 5.6.
Określenie, czy dany przypadek jest typu NC lub CC jest niezbędne do analizy oscylacji. W eksperymencie MINOS zjawisko oscylacji badane jest w oparciu o oddziaływania CC neutrin mionowych. Oprócz tego niezbędne jest także posiadanie informacji o przypadkach NC, które stanowią tło dla CC νμ.
W rozdziale 5.1 przedstawiono graficznie podstawowe różnice między oddziaływaniami NC i CC. W najprostszej wersji przypadek NC charakteryzuje jedna kaskada hadronowa. W oddziaływaniu CC νμ oprócz kaskady rejestrowany jest także tor mionu. Najprostszym kryterium rozdziału oddziaływań NC oraz CC νμ jest stwierdzenie, czy widoczny jest tor mionu czy nie. Problem pojawia się w przypadku neutrin niskoenergetycznych, kiedy to wyprodukowany mion posiada bardzo krótki tor nie wychodzący poza obręb kaskady hadronowej. Dodatkowym utrudnieniem może być także błędna rekonstrukcja sygnału, kiedy to np. w przypadku NC zostanie zrekonstruowany fikcyjny tor.
Na podstawie wymienionych w poprzednim podrozdziale zmiennych, opracowano tzw. metodę cięć selekcji przypadków CC i NC. Dzieli się ona na dwa oddzielne algorytmy: algorytm zoptymalizowany na samą selekcję CC oraz na samą selekcję NC. Na potrzeby ninieszej pracy powstał program komputerowy dokonujący selekcji przypadków i obrazujący wyniki w postaci histogramów i wykresów. Przeanalizowano 69685 wysymulowanych przypadków MonteCarlo. Dokłady opis stworzonego programu znajduje się w dodatku B.
Schemat algorytmu selekcji z optymalizacją na CC:
- zmienna 1 ≤ 0,07 ⇒ tło
- zmienna 1 ≥ 0,25 ⇒ CC
- zmienna 2 ≤ 9 ⇒ tło
- zmienna 2 ≥ 14 ⇒ CC
- zmienna 3 ≤ 8000 ⇒ tło
- zmienna 3 ≤ 28000 ⇒ CC
- pozostałe przypadki oznaczone jako UNKNOWN (z angielskiego nieznane)
- zmienna 1 ≥ 0,5 ⇒ tło
- zmienna 1 ≤ 0,12 ⇒ NC
- zmienna 2 ≥ 30 ⇒ tło
- zmienna 2 ≤ 9,5 ⇒ NC
- (zmienna 3 ≤ 7000 lub zmienna 3 ≥ 69000) ⇒ NC
- pozostałe przypadki oznaczone jako UNKNOWN
Dany przypadek zaklasyfikowany jest jako CC, gdy wartość kolejnej zmiennej dla przypadku spełnia postawiony warunek. W przeciwnym razie przechodzi do następnej zmiennej w celu dalszej analizy. Dlatego też po każdym następnym cięciu rozpatrywana jest już wiązka pomniejszona o liczbę przypadków zaklasyfikowanych jedno cięcie wcześniej.
Część oddziaływań, które ewidentnie nadają się na NC, oznaczono jako tło. Ma to na celu usunięcie wielu niepotrzebnych przypadków, które, przechodząc do następnego cięcia, istotnie utrudniałyby selekcję. Status przypadków tła oraz UNKNOWN jest taki sam, czyli są bezpowrotnie usuwane z danej analizy. Jest ich 22% spośród wszystkich przypadków, z czego sam status UNKNOWN ma tylko 0,005%.
Wszystkie powyższe cięcia można zobrazować na histogramach poszczególnych zmiennych (rys. od 5.8 do 5.10). Wszystkie histogramy zostały wygenerowane tylko dla przypadków jeszcze nie zaklasyfikowanych.
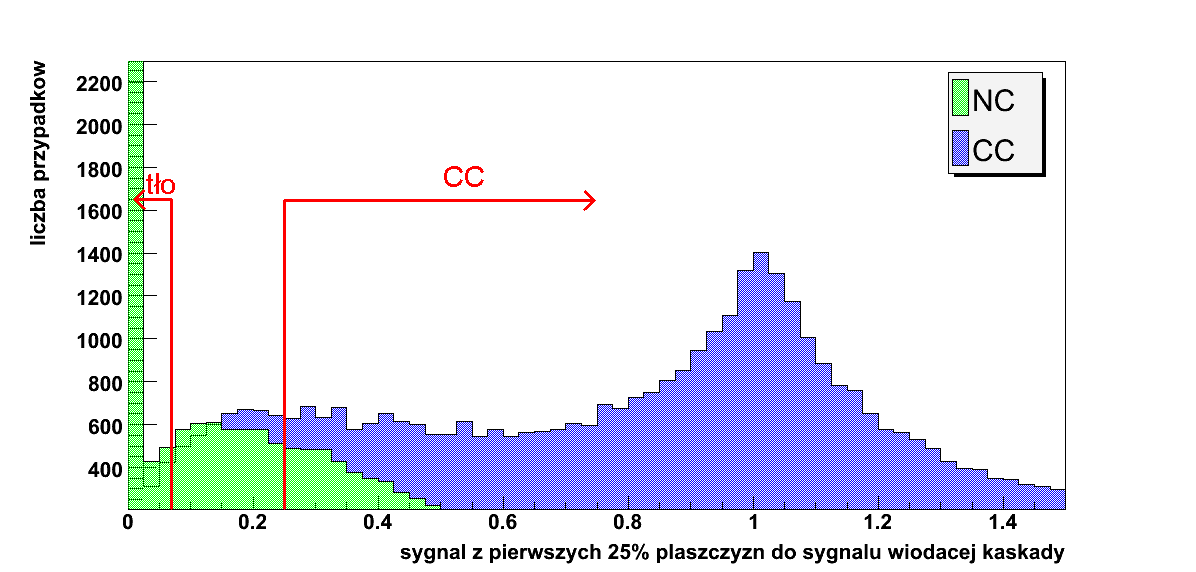
Rysunek 5.8: Zmienna 1: sygnał z pierwszych 25% płaszczyzn podzielony przez sygnał wiodącej kaskady
 |
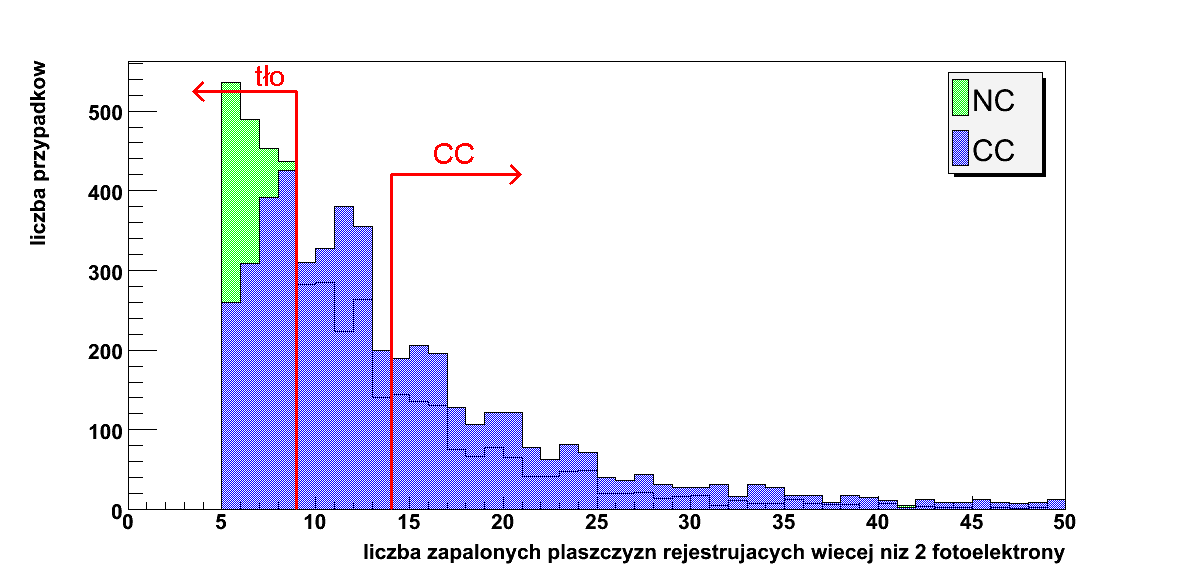
Rysunek 5.9: Zmienna 2: liczba zapalonych płaszczyzn rejestrujących wiecej niż 2 fotoelektrony po poprzednich cięciach
 |
Rysunek 5.10: Zmienna 3: sygnał wiodącego toru po poprzednich cięciach
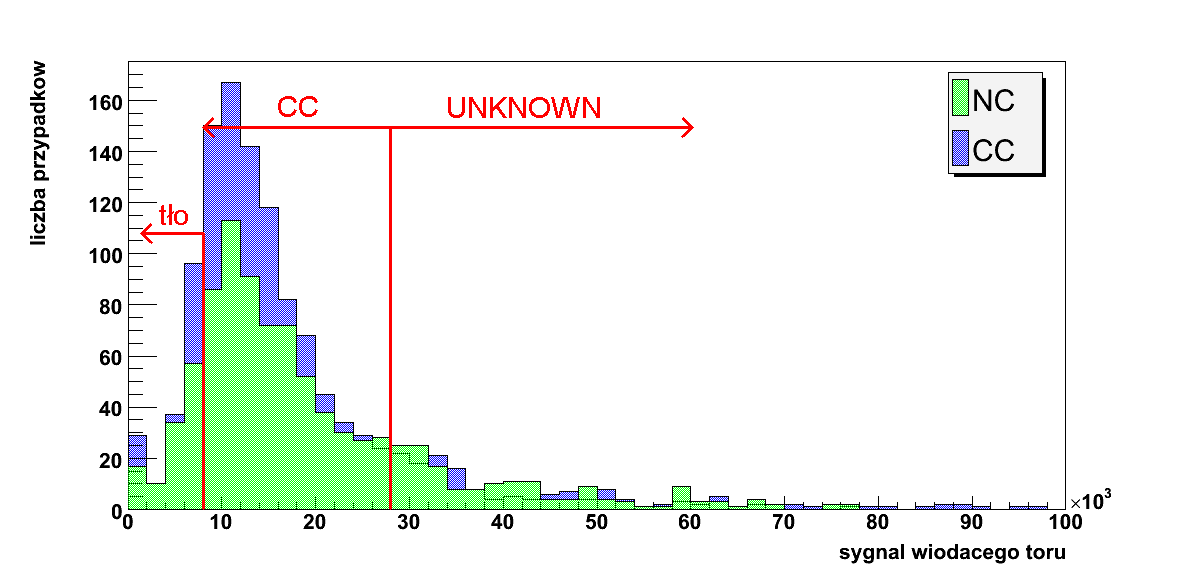 |
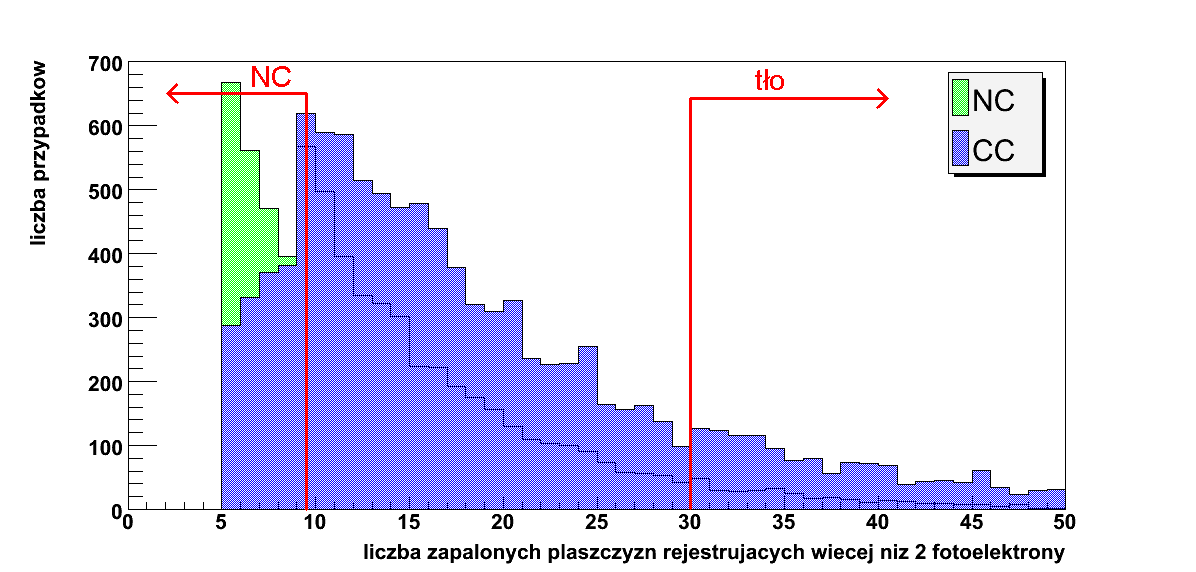
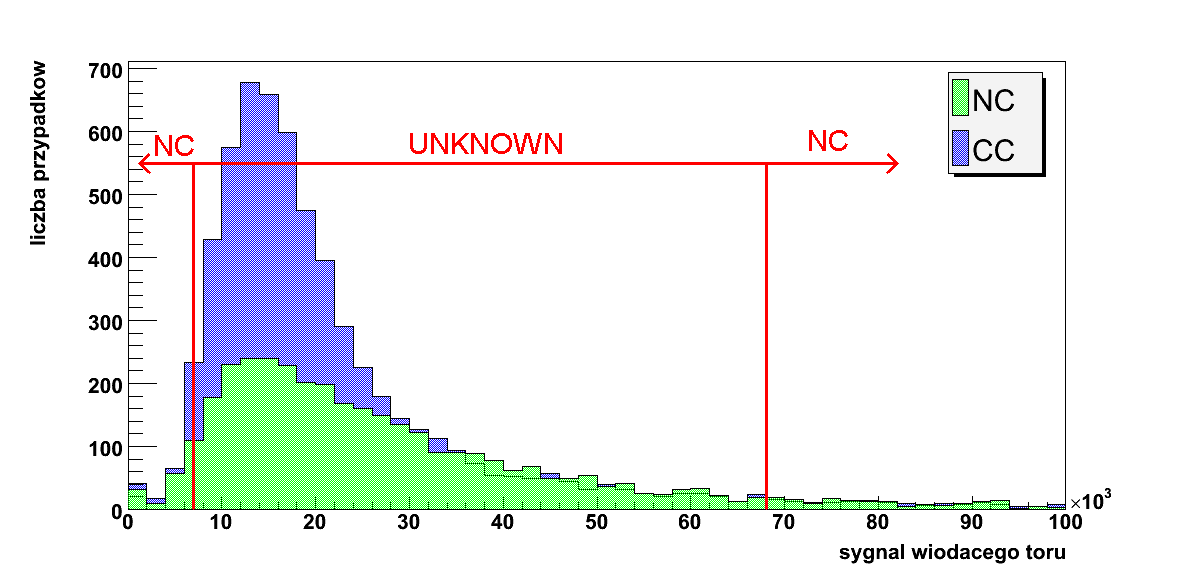
Na powyższych histogramach czerwoną kreską oznaczono miejsce ciecia na danej zmiennej. Obszar zaznaczony strzałką został przez algorytm zaklasyfikowany jako CC, tło lub UNKNOWN.
Schemat algorytmu selekcji z optymalizacją na NC:
Przypadków oznaczonych jako tło jest 60%, a jako UNKNOWN 13%.
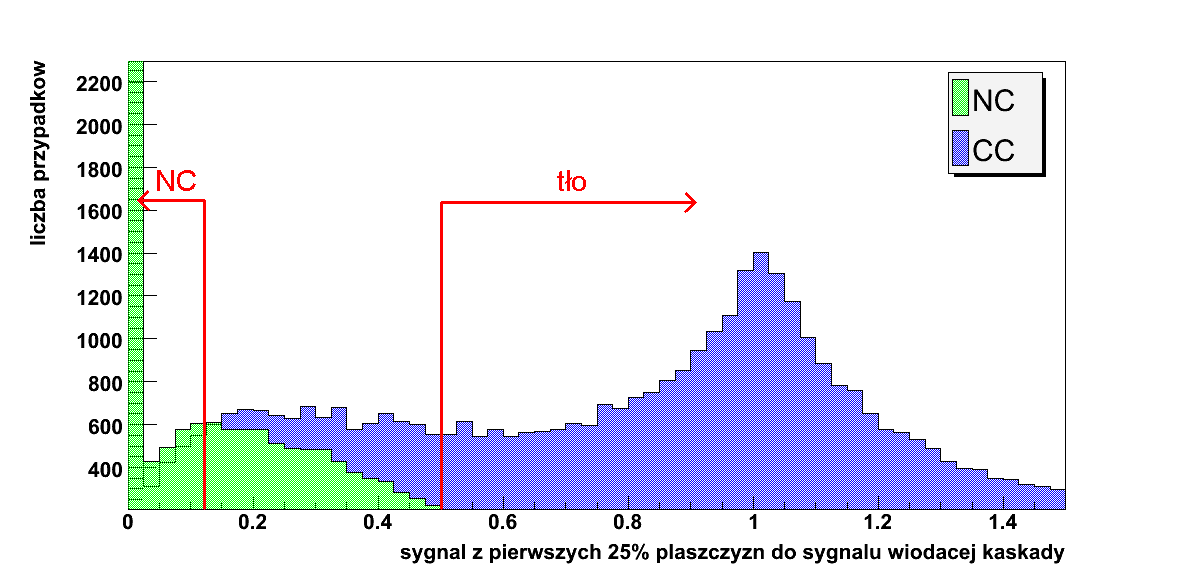
Stosując analogiczną metodę jak w przypadku optymalizacji na CC, zobrazowano miejsca cięć na rys. od 5.11 do 5.13.
Rysunek 5.11: Zmienna 1: sygnał z pierwszych 25% płaszczyzn podzielony przez sygnał wiodącej kaskady
 |
Rysunek 5.12: Zmienna 2: liczba zapalonych płaszczyzn rejestrujących wiecej niż 2 fotoelektrony po poprzednich cięciach
 |
Rysunek 5.13: Zmienna 3: sygnał wiodącego toru po poprzednich cięciach
 |
komentarze
Copyright © 2008-2010 EPrace oraz autorzy prac.