
Prawdopodobieństwo oscylacji νμ → ντ
Prawdopodobieństwo oscylacji dowolnego neutrina να w νβ o energii E w odległości L od źródła opisywane jest wzorem ([11]):
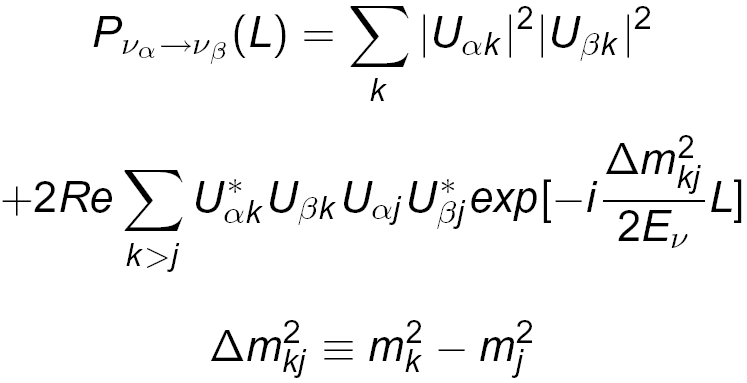 gdzie i oraz j są liczbami od 1 do 3, a U jest macierzą oscylacji. Dla prawdopodobieństwa oscylacji neutrin mionowych w neutrina taonowe w eksperymencie MINOS, powyższy wzór przyjmuje uproszczoną postać:
gdzie i oraz j są liczbami od 1 do 3, a U jest macierzą oscylacji. Dla prawdopodobieństwa oscylacji neutrin mionowych w neutrina taonowe w eksperymencie MINOS, powyższy wzór przyjmuje uproszczoną postać:

gdzie Θ23 oznacza kąt mieszania stanów 2 i 3, a 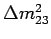 różnicę kwadratów mas pomiędzy stanami 2 i 3 [28] [2].
różnicę kwadratów mas pomiędzy stanami 2 i 3 [28] [2].
Ze wzoru na prawdopodobieństwo oscylacji wyprowadzić można wzór na prawdopodobieństwo zachowania pierwotnej wiązki jako:
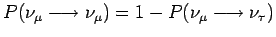
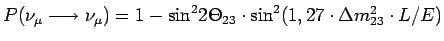
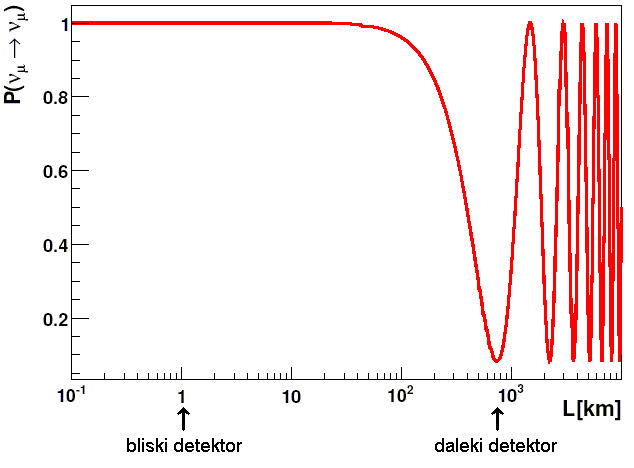
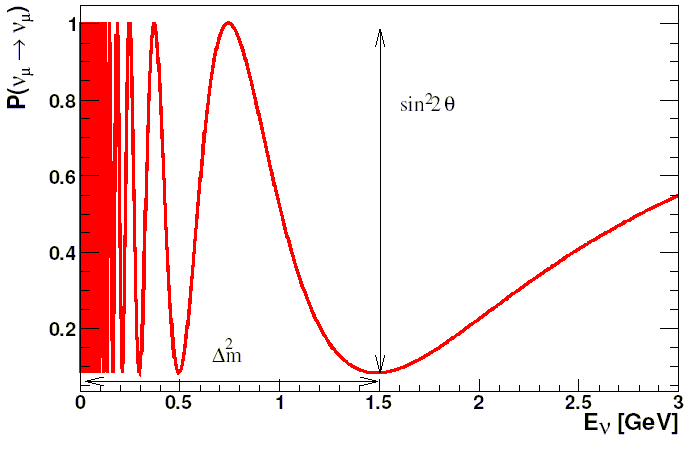
Na rysunkach 4.4 i 4.5 znajdują się teoretyczne wykresy prawdopodobieństwa
P(νμ → νμ) w funkcji L (rys. 4.4) oraz energii neutrin E (rys. 4.5 - jest to tzw. krzywa oscylacyjna). Bliski detektor został ustawiony w takiej odległości, aby oscylacje jeszcze nie zachodziły. Z kolei daleki detektor jest umieszczony w okolicy oczekiwanego maksimum oscylacji (rys. 4.4), aby zaobserwowany efekt był jak największy. Z krzywej oscylacji można wyznaczyć parametry oscylacji sin22Θ oraz Δm2 (rys. 4.5).
Rysunek 4.4: Prawdopodobieństwo zachowania pierwotnego zapachu neutrina w zależności od odległości od źródła neutrin [11]
 |
Rysunek 4.5: Prawdopodobieństwo zachowania pierwotnego zapachu neutrina w zależności od energii. Strzałkami zostały oznaczone dwie wielkości: głębokość minimum jest miarą sin22Θ, a położenie minimum mówi o Δm2 [11]
 |
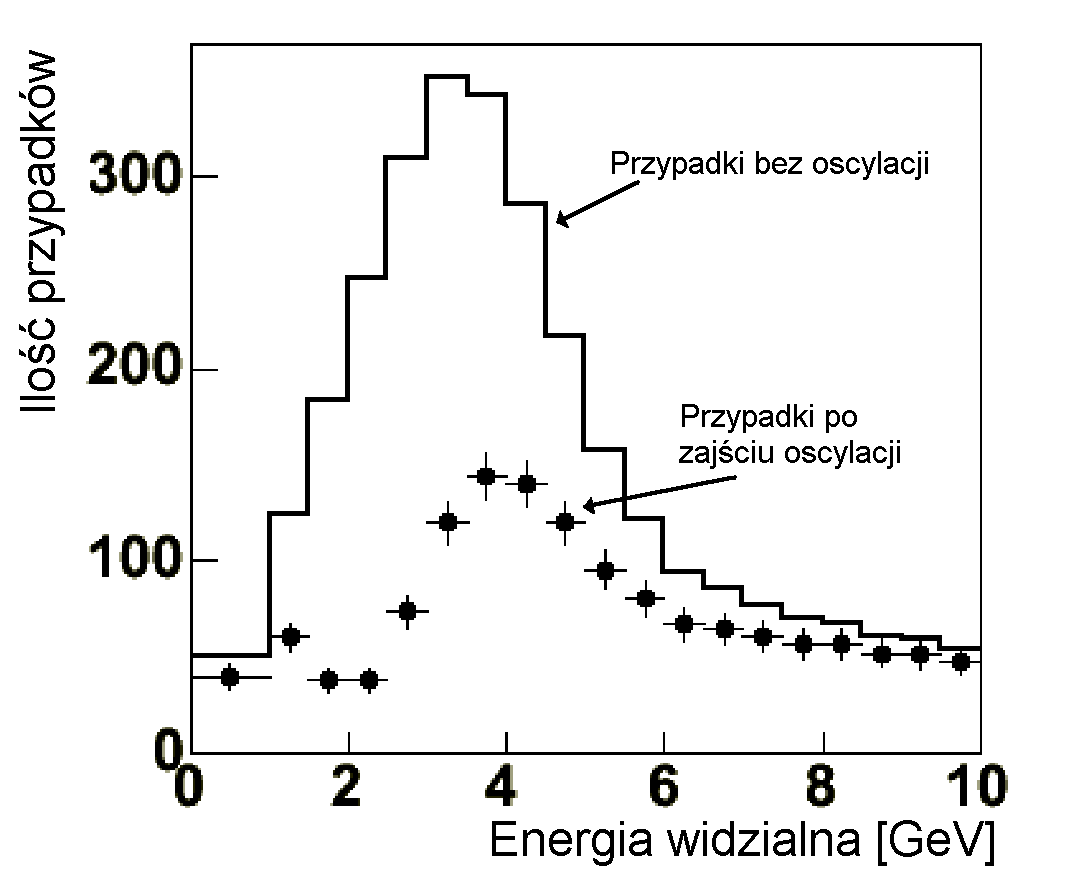
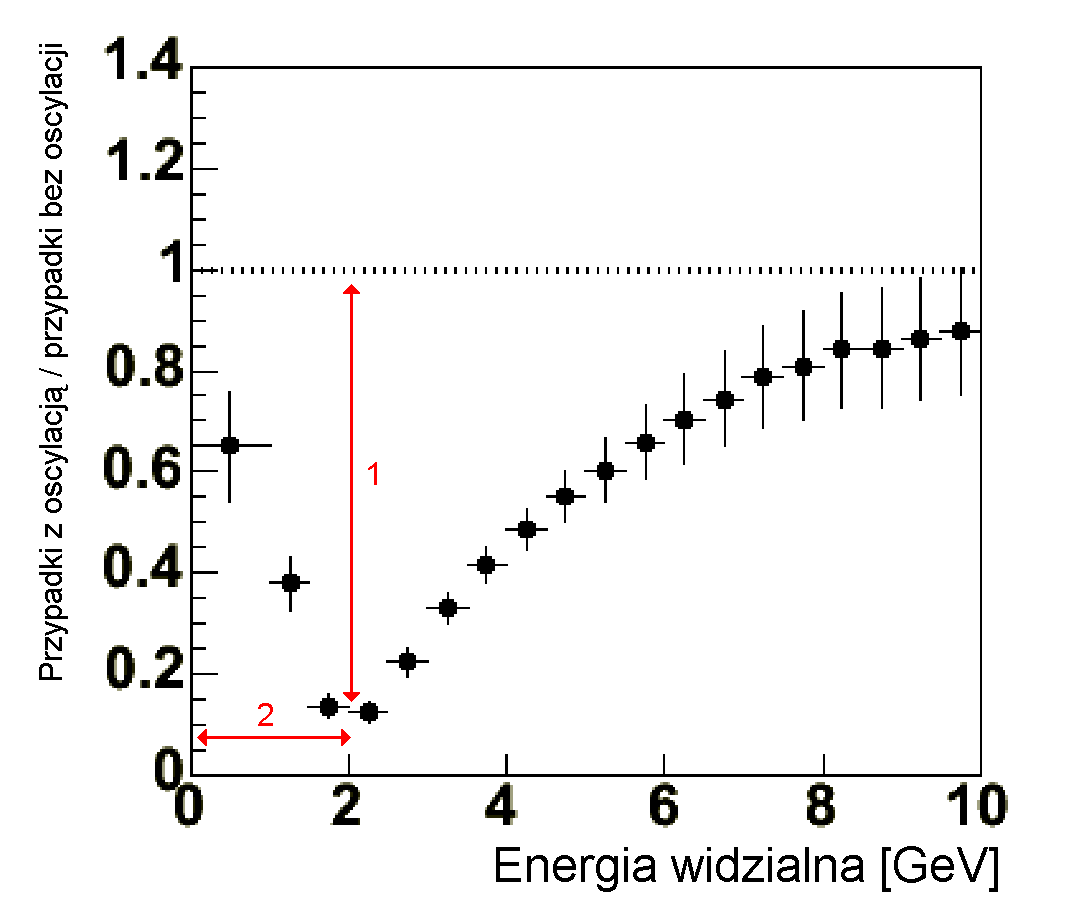
Na wykresach 4.6 przedstawiono rozkłady wysymulowanych przypadków oddziaływań neutrin mionowych w funkcji energii dla eksperymentu MINOS dla dalekiego detektora. Na lewym wykresie zawarto dwa histogramy. Pierwszy, poprowadzony linią ciągłą, przedstawia oczekiwaną wiązkę neutrin w przypadku, gdyby oscylacje nie zachodziły. Drugi histogram, złożony z punktów, przedstawia rozkład po zajściu zjawiska oscylacji. Na prawym wykresie podzielono histogramy z lewej ilustracji otrzymując stosunek przypadków po oscylacji i bez niej (krzywa oscylacyjna). Głębokość minimum oznaczona czerwoną cyfrą '1' mówi o wartości sin22Θ23, natomiast położenie minimum oznaczone '2' wyznacza 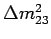 (patrz także rys. 4.5, na którym przedstawiono teoretyczną krzywą oscylacyjną). Oznacza to, iż w sposób jednoznaczny można zbadać zjawisko oscylacji neutrin analizując przypadki w dalekim detektorze eksperymentu MINOS, znając jednocześnie energię wiązki E oraz odległośc L między samymi detektorami [8].
(patrz także rys. 4.5, na którym przedstawiono teoretyczną krzywą oscylacyjną). Oznacza to, iż w sposób jednoznaczny można zbadać zjawisko oscylacji neutrin analizując przypadki w dalekim detektorze eksperymentu MINOS, znając jednocześnie energię wiązki E oraz odległośc L między samymi detektorami [8].
Rysunek 4.6: Wykresy ilustrujące zjawisko oscylacji νμ w eksperymencie MINOS w oparciu o Monte Carlo. Lewy: oczekiwany rozkład energii w dalekim detektorze, gdyby oscylacji nie było (czarna linia) oraz po jej zajściu (czarne punkty); prawy: krzywa oscylacyjna powstała w wyniku podzielenia wykresów z rysunku lewego [10]
  |
Eksperyment MINOS w dalszym ciągu zbiera dane powiększając zebraną już statystykę oraz udoskonalając analizę przypadków. W lipcu 2007 roku [12] ogłoszone zostały wyniki dotyczące parametrów oscylacji:
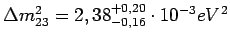
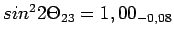
Powyższe wyniki bazują na statystyce 2,5 * 1020 pot (ang. Protons On Target, protonów na tarczę).
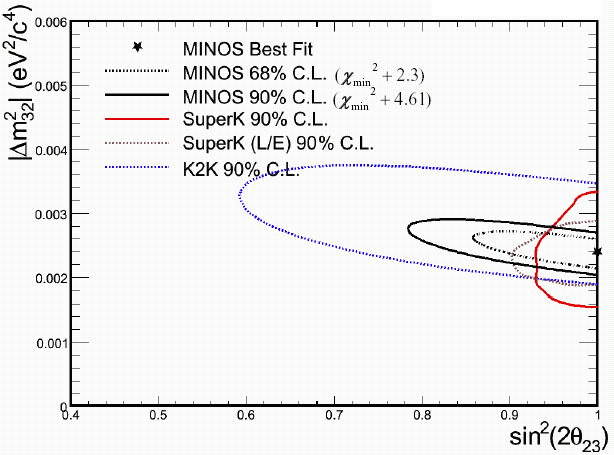
Rysunek 4.7 przedstawia przestrzeń parametrów oscylacji z zaznaczonymi aktualnymi wynikami eksperymentu MINOS w porównaniu z wynikami dla eksperymentów Super-K oraz K2K. W chwili obecnej precyzja wyników MINOS'a jest większa niż w K2K, a w przypadku pomiaru Δ m2 lepsza niż w Super-K. W przyszłości wyniki te zostaną jeszcze bardziej poprawione.
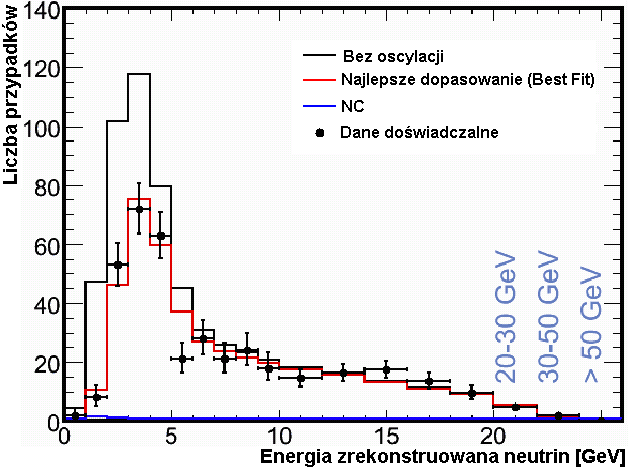
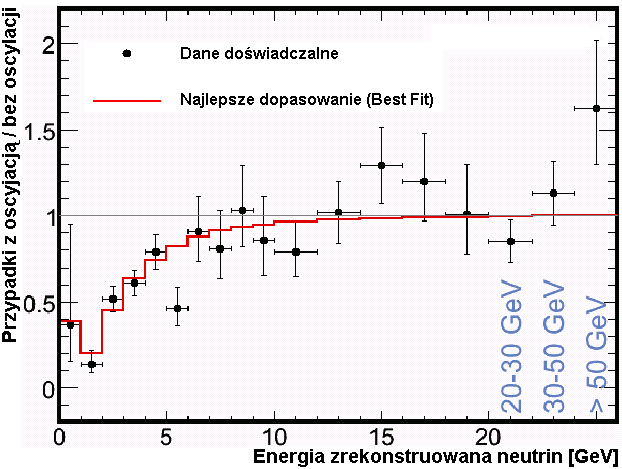
Rysunek 4.8 przedstawia zmierzoną krzywą oscylacyjną w oparciu o dane eksperymentalne i jest odpowiednikiem rys. 4.6 dla MC.
Rysunek 4.7: Oficjalne wyniki eksperymentu MINOS z 19 lipca 2007 r. z wynikami dla eksperymentów Super-K oraz K2K [12]
 |
Rysunek 4.8: Wykresy ilustrujące zjawisko oscylacji νμ w eksperymencie MINOS. Lewy: rozkład energii przed i po oscylacji; prawy: krzywa oscylacyjna powstała w wyniku podzielenia wykresów z rysunku lewego [12]
  |
komentarze
Copyright © 2008-2010 EPrace oraz autorzy prac.