
Uproszczony model oscylacji
Do pełnego zrozumienia mechanizmu oscylacji neutrin posłużmy się modelem uproszczonym zakładającym istnienie tylko dwóch stanów masowych ν1, ν2 i dwóch hipotetycznych stanów zapachowych να, νβ. Załóżmy także, iż stan νβ składa się w większej części ze stanu ν2, a stan να głównie z ν1. Wprowadzając kąt Θ jako kąt mieszania między stanami masowymi, zapisać można tzw. macierz mieszania:
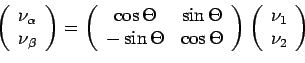
Powyższy zapis można lepiej zrozumieć analizując rysunek 4.2. Przedstawia on graficzne zależności pomiędzy stanami zapachowymi a masowymi przy kącie mieszania Θ.
Rysunek 4.2: Schemat mieszania stanów neutrinowych [4]
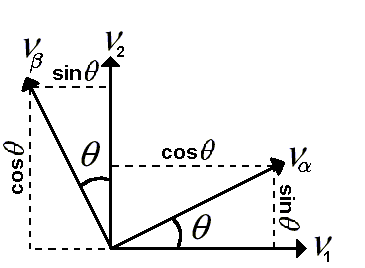 |
Macierz mieszania można przedstawić za pomocą stanów kwantowych neutrin:
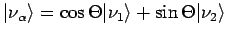
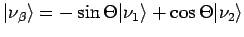
Widać zatem jak bardzo zapach neutrina (α bądź β) zależy od kąta mieszania Θ. Im Θ jest mniejsze, tym cos Θ jest bliższy wartości 1, a co za tym idzie να składa się głównie ze stanu ν1. Analogicznie νβ składa się prawie wyłącznie ze stanu ν2.
Kąt Θ może przyjmować dowolne wartości z przedziału (0,π/4). Gdyby Θ było równe maksymalnej wartości π/4, wówczas oba zapachy α i β posiadałyby procentowo tyle samo stanu ν1 i ν2. W przypadku Θ = 0 zjawisko oscylacji by nie zachodziło. Propagacja w czasie funkcji falowych ν1 i ν2 zależy od energii E. Jeżeli stany mają różne masy, to różne też będą prędkości propagacji. Otrzymuje się wówczas wzajemną interferencję obu fal - raz konstruktywną a raz destruktywną (rys. 4.3). Po przebyciu drogi L prawdopodobieństwo, że να pozostanie να, wynosi:
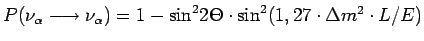
gdzie jednostki L[m], Δm2[eV2] i E[MeV] [2]. Zapach neutrina jest więc funkcją odległości pokonanej przez wiązkę neutrin (rys. 4.3) [28] [4].
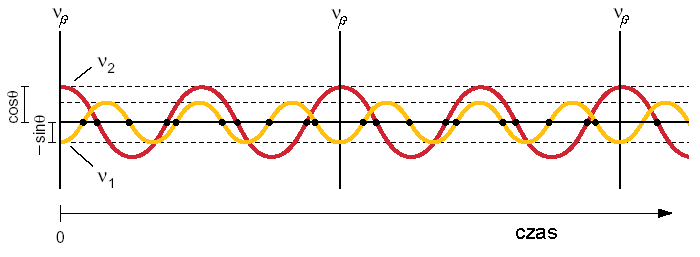
Rysunek 4.3: Schemat oscylacji dwóch typów neutrin, ukazujący amplitudy stanów własnych masy ν1 i ν2, dla dwóch zapachów neutrin να i νβ [4]
 |
komentarze
Copyright © 2008-2010 EPrace oraz autorzy prac.